행렬은 뭔가요?

1. 행렬(matrix)은 벡터를 원소로 가지는 2차원 배열입니다

X3,3

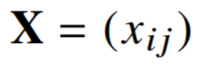
• 행렬의 특정행(열)을 고정하면 행(열)벡터라 부릅니다

1. 행렬은 벡터공간에서 사용되는 연산자(operator)로 이해한다
2. 행렬곱을 통해 벡터를 다른 차원의 공간으로 보낼 수 있다
3. 행렬곱을 통해 패턴을 추출할 수 있고 데이터를 압축할 수 있다

 

2. 전치행렬

•  

  

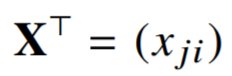
  전치행렬은 행과 열이 바뀐 행렬

   
• 벡터가 공간에서 한점을 의미한다면 행렬은 여러점들을 의미함

 

행렬의 행벡터 xi는 i번째 데이터를 의미

•  

  

3. 행렬의 곱

• 행렬곱셈(matrixmultiplication)은 i번째 행벡터와 j번째 열벡터 사이의 내적을 성분으로 가지는 행렬을 계산합니다

 

4. 행렬의 내적

• np.inner는 i번째 행벡터와 j번째 행벡터 사이의 내적을 성분으로 가지는 행렬을 계산

행렬의 내적

5. 역행렬

numpy.linalg.inv 로 구할 수 있다

• 만일 역행렬을 계산할 수 없다면 유사역행렬(pseudo-inverse) 또는 무어펜로즈(Moore-Penrose)역행렬을 이용한다

  

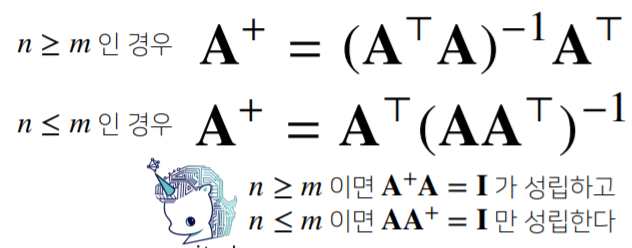
  무어펜로즈 역행렬

무어펜로즈 역행렬은 numpy.linalg.pinv로 구할 수 있다

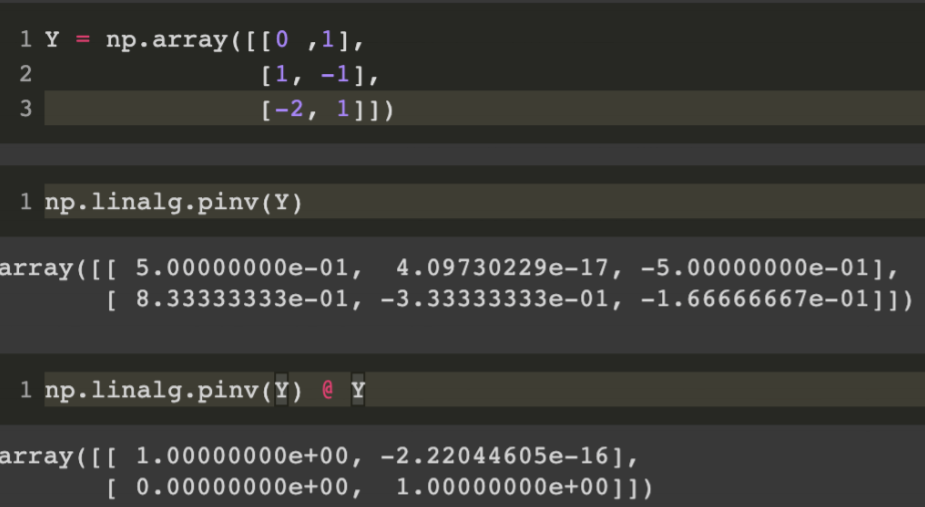
6. 응용

• 1. np.linalg.pinv를 이용하면 연립방정식의 해를 구할 수 있다
  • a11 x1 + a12 x2 + ··· + a1n x n = b1
  • a21 x1 + a22 x2 + ··· + a2n xn = b2
• Ax =B 행렬로 바꾸어 계산

 

• 2. np.linalg.pinv를 이용하면 데이터를 선형모델(linearmodel)로 해석하는 선형회귀식을 찾을 수 있다

•