경사하강법
2021. 8. 6. 15:03ㆍ네이버 부스트캠프 AI tech 2기
728x90
1. 경사상승법 / 경사하강법 (gradient ascent/descent)
경사상승법
- 함수증가 -> 미분값을 더함 = x+f'(x)

경사하강법
- 함수감소 -> 미분값으 뺌 = x-f'(x)

경사상승/경사하강 방법은 극값에 도달하면 움직임을 멈춘다
- 극값에서는 미분값이 0이므로
- 목적함수 최적화 종료
- 점이 이동 하며 얻은 미분 값의 합/차
- 미분값을 더해줌 -> 함수의 최대화
- 미분값을 빼붐 -> 함수의 최소화
- 최대/최소 값일 때 움직임을 멈춤(극값에 도달)
- 최적화
- 알고리즘 학습률 조정을 통해 학습속도 조절

2. 그레디언트 벡터
- 다차원에서의 극값을 찾음
- (x, y, z) --> (x', y', z')
- 벡터가 입력인 다변수 함수는 편미분을 사용


나블라 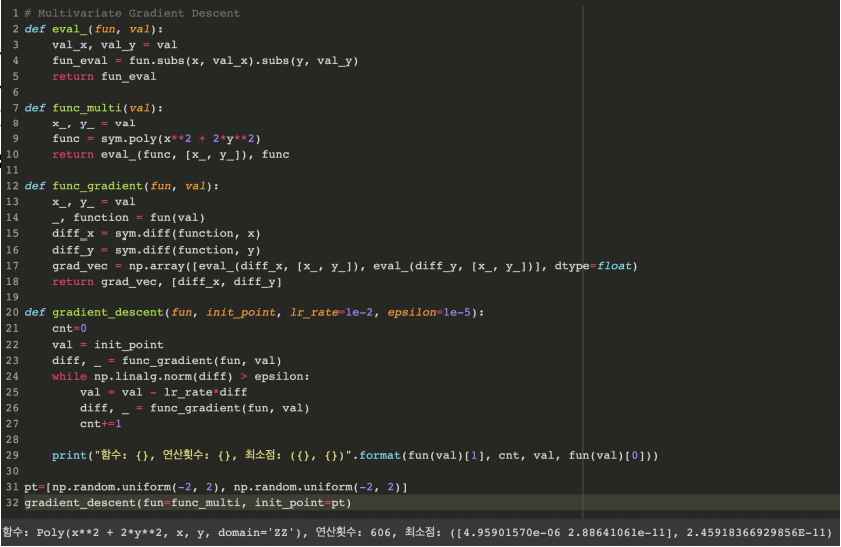
- 그레디언트 벡터 ∇f(x, y)는 각 점(x,y)에서 가장 빨리 증가하는 방향으로 흐른다
- 그레디언트 벡터 -∇f는 각 점에서 가장 빨리 감소하는 방향으로 흐른다
3. 경사하강법으로 선형회귀 계수 구하기
- 선형회귀의 목적식은 ∥y − Xβ∥2이고 이를 최소화하는 β찾아야함.
- ∥y − Xβ∥2 -> L2노름
- 목적식을 최소화하는 β를 구하는 경사하강법 알고리즘


경사하강법기반 선형회귀 알고리즘 - 경사하강법 알고리즘에서는 학습률과 학습횟수가 중요한 hyperparameter이다.
- 미분가능, 볼록(convex)한 함수에 적절한 학습률과 학습횟수를 선택하면 수렴이 보장됨
- 하지만 비선형회귀 문제는 목적식이 볼록하지 않으므로 수렴이 보장되지 않음
4. 확률적 경사하강법(SGD)
확률적 경사하강법은 데의터의 일부만 활용하여 업데이트
- 볼록이 아닌 목적식은 SGD를 통해 최적화
- SGD는 미니배치(부분집합)를 가지고 그레디언트 벡터를 계산
- 미니배치는 확률적으로 선택하므로 매번 목적식 모양이 바뀜
- 머신러닝 학습에 효율적
728x90
'네이버 부스트캠프 AI tech 2기' 카테고리의 다른 글
| 행렬은 뭔가요? (0) | 2021.08.06 |
|---|---|
| AI math 1. 벡터가 뭔가요? (0) | 2021.08.06 |
| AI tech 1일차 (0) | 2021.08.03 |